


Next: F.E.M. periódica
Up: Resolvendo a equação
Previous: Resolvendo a equação
Para achar uma solução particular da Eq. 13
precisamos
especificar 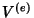 em detalhe. Seja, para começar,
em detalhe. Seja, para começar, 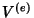 constante
(como uma pilha de 1,5 Volts, por exemplo). Então
constante
(como uma pilha de 1,5 Volts, por exemplo). Então
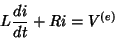 |
(15) |
possui a solução
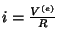 . A solução geral da
Eq. 13 é, então,
. A solução geral da
Eq. 13 é, então,
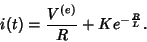 |
(16) |
Para 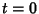 , temos
, temos
Logo,
Segue que
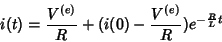 |
(17) |
Temos nesta solução um termo que decresce com o tempo, terminando
por desaparecer.
É o chamado ``transiente'': para 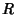 fixo, o transiente é tanto mais
duradouro
quanto maior for
fixo, o transiente é tanto mais
duradouro
quanto maior for 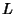 , A indutância, portanto, tem um caráter de
inércia,
opondo-se ao desaparecimento do transiente. Esgotado o transiente,
permanece a corrente
estacionária, cujo valor é
, A indutância, portanto, tem um caráter de
inércia,
opondo-se ao desaparecimento do transiente. Esgotado o transiente,
permanece a corrente
estacionária, cujo valor é
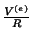 .
.
Henrique Fleming
2001-11-29