


Next: Circuitos RLC
Up: Resolvendo a equação
Previous: F.E.M. constante
O caso mais interessante é o de uma
força eletromotriz
periódica,
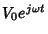 (usamos
(usamos 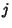 como
como 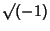 para não
confundir
com a corrente, denotada por
para não
confundir
com a corrente, denotada por 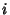 ). Para achar uma solução
particular de
). Para achar uma solução
particular de
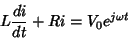 |
(18) |
tentamos
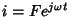 , com
, com 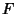 a determinar. Como, então,
a determinar. Como, então,
obtemos, para a Eq. 18,
Cancelando a exponencial obtém-se facilmente
ou seja,
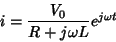 |
(19) |
Note que
de maneira que
Levando em 19 , temos
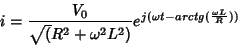 |
(20) |
ou, finalmente, tomando a parte real,
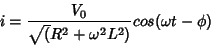 |
(21) |
com
A solução geral da Eq. 13 será, então,
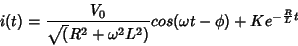 |
(22) |
onde se identificam claramente a corrente estacionária periódica
e o termo transiente.



Next: Circuitos RLC
Up: Resolvendo a equação
Previous: F.E.M. constante
Henrique Fleming
2001-11-29