Next: Apêndice
Up: A magia da equação
Previous: Máximos e mínimos
Como aplicações desses poderosos teoremas, vamos resolver completamente
o seguinte problema: uma carga puntifome de valor 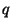 é posta a uma
distância
é posta a uma
distância 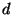 do centro de uma esfera condutora de raio
do centro de uma esfera condutora de raio 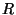 . A carga é
externa à esfera, ou seja,
. A carga é
externa à esfera, ou seja, 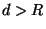 . Determinar o campo elétrico resultante.
Primeiramente, vamos supor que a esfera esteja ligada à terra, que é uma
linguagem técnica para dizer que o potencial na esfera é mantido igual a zero.
Este problema não é do tipo que pode ser resolvido pelo uso da solução da
equação de Poisson dada por
. Determinar o campo elétrico resultante.
Primeiramente, vamos supor que a esfera esteja ligada à terra, que é uma
linguagem técnica para dizer que o potencial na esfera é mantido igual a zero.
Este problema não é do tipo que pode ser resolvido pelo uso da solução da
equação de Poisson dada por
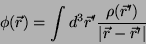 |
(23) |
porque não conhecemos a distribuição de cargas que aparecem no condutor
por causa da presença da carga 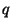 externa. Por outro lado, sabemos que, fora
do condutor, só existe a carga
externa. Por outro lado, sabemos que, fora
do condutor, só existe a carga 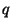 , e que, portanto, fora do condutor (e excluído
o ponto onde está a carga
, e que, portanto, fora do condutor (e excluído
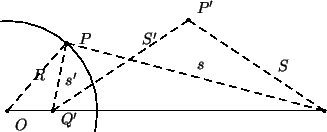
o ponto onde está a carga 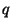 ), a equção de Laplace é satisfeita. A figura abaixo
descreve a situação.
A primeira aplicação do teorema de unicidade da equação de Laplace a este caso é
muito simples: determinar o potencial em todos os pontos no interior da esfera
condutora. Como o condutor está em equilíbrio, sabemos que sua superfície
é uma equipotencial; além disso, como está ligado à terra, o valor desse potencial
constante é zero, pelo menos na superfície. Considere a região interna ao condutor,
limitada, isto é, pela superfície (fechada) do mesmo. Para esta região só existe
uma solução com valor zero na superfície, pelo teorema da unicidade. Ora, a função
que tem valor zero em todos os pontos do interior satisfaz obviamente, aí, a equação
de Laplace, e tem o valor zero na superfície. Então, resolve o problema, e é
a única solução.
Pode-se usar este método também para a região externa à esfera, com algum
cuidado. Primeiro, consideremos a superfície complexa (isto é, composta de
várias partes) formada por: a superfície esférica da figura; uma pequeniníssima
superfície esférica em torno da carga
), a equção de Laplace é satisfeita. A figura abaixo
descreve a situação.
A primeira aplicação do teorema de unicidade da equação de Laplace a este caso é
muito simples: determinar o potencial em todos os pontos no interior da esfera
condutora. Como o condutor está em equilíbrio, sabemos que sua superfície
é uma equipotencial; além disso, como está ligado à terra, o valor desse potencial
constante é zero, pelo menos na superfície. Considere a região interna ao condutor,
limitada, isto é, pela superfície (fechada) do mesmo. Para esta região só existe
uma solução com valor zero na superfície, pelo teorema da unicidade. Ora, a função
que tem valor zero em todos os pontos do interior satisfaz obviamente, aí, a equação
de Laplace, e tem o valor zero na superfície. Então, resolve o problema, e é
a única solução.
Pode-se usar este método também para a região externa à esfera, com algum
cuidado. Primeiro, consideremos a superfície complexa (isto é, composta de
várias partes) formada por: a superfície esférica da figura; uma pequeniníssima
superfície esférica em torno da carga 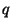 ; uma outra superfície esférica,
concêntrica com a primeira, e de raio muitíssimo grande. Orientemos as
três superfícies assim: a esfera condutora, com a normal interna; a pequena
esfera, com a normal interna; a enorme esfera, com a normal externa. Juntas e
orientadas assim, elas são a ``superfície externa'' do volume externo ao
condutor e à esferinha, e interno à esferona. Neste volume não há cargas,
logo, o potencial satisfaz a equação de Laplace. Além disso, temos as seguintes condições
sobre os ``contornos'' (que são as superfícies citadas): sobre o condutor,
; uma outra superfície esférica,
concêntrica com a primeira, e de raio muitíssimo grande. Orientemos as
três superfícies assim: a esfera condutora, com a normal interna; a pequena
esfera, com a normal interna; a enorme esfera, com a normal externa. Juntas e
orientadas assim, elas são a ``superfície externa'' do volume externo ao
condutor e à esferinha, e interno à esferona. Neste volume não há cargas,
logo, o potencial satisfaz a equação de Laplace. Além disso, temos as seguintes condições
sobre os ``contornos'' (que são as superfícies citadas): sobre o condutor,
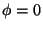 ; sobre a esferinha de raio
; sobre a esferinha de raio 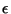 ,
,
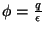 ,
sobre a esferona,
,
sobre a esferona, 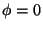 (ela é muuuito grande!). Posteriormente fazemos o raio
da esfera grande tender ao infinito. Então podemos usar o teorema da unicidade
para essar região. Se acharmos uma função que satisfaça a esuqção de
Laplace na região e tenha os valores estipulados nas siperfícies, essa será
a solução única.
William Thomson, Lord Kelvin1
teve uma de suas idéias geniais: percebeu que
poderia obter um potencial com as propriedades acima trabalhando com uma
distribuição de cargas muito simples: simplesmente adicionando, à carga
(ela é muuuito grande!). Posteriormente fazemos o raio
da esfera grande tender ao infinito. Então podemos usar o teorema da unicidade
para essar região. Se acharmos uma função que satisfaça a esuqção de
Laplace na região e tenha os valores estipulados nas siperfícies, essa será
a solução única.
William Thomson, Lord Kelvin1
teve uma de suas idéias geniais: percebeu que
poderia obter um potencial com as propriedades acima trabalhando com uma
distribuição de cargas muito simples: simplesmente adicionando, à carga 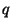 ,
uma carga
,
uma carga 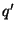 , de valor a ser determinado, na posição
, de valor a ser determinado, na posição 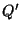 (veja a figura). O que
esta posição tem de especial é que o ponto
(veja a figura). O que
esta posição tem de especial é que o ponto 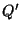 é escolhido de tal forma que
o triângulo
é escolhido de tal forma que
o triângulo 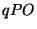 seja semelhante ao triângulo
seja semelhante ao triângulo 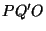 . Vamos mostrar que
o potencial criado só por essas duas cargas tem as propriedades desejadas (no
exterior da esfera condutora). De fato, sendo o potencial de duas cargas puntiformes,
ele satisfaz a equação de Laplace em todos os pontos, menos aqueles onde as
cargas estão. Portanto, em toda a região descrita. Além disso, ele se anula
no infinito, e o leitor não terá dificuldades para provar que, numa superfície
esférica infinitamente próxima de
. Vamos mostrar que
o potencial criado só por essas duas cargas tem as propriedades desejadas (no
exterior da esfera condutora). De fato, sendo o potencial de duas cargas puntiformes,
ele satisfaz a equação de Laplace em todos os pontos, menos aqueles onde as
cargas estão. Portanto, em toda a região descrita. Além disso, ele se anula
no infinito, e o leitor não terá dificuldades para provar que, numa superfície
esférica infinitamente próxima de 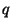 , o potencial é
, o potencial é
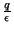 . Resta
mostrar que este potencial é zero na superfície da esfera condutora. Isto
também é facil. Sejam
. Resta
mostrar que este potencial é zero na superfície da esfera condutora. Isto
também é facil. Sejam 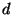 e
e 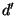 , respectivamente, as distâncias do ponto
, respectivamente, as distâncias do ponto 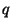 e do ponto
e do ponto 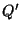 ao centro da esfera. Mostra-se facilmente, da semelhança de
triângulos, que
ao centro da esfera. Mostra-se facilmente, da semelhança de
triângulos, que
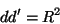 |
(24) |
Ainda da semelhança de triângulos segue que
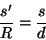 |
(25) |
ou
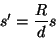 |
(26) |
Suponhamos que exista uma carga 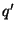 no ponto
no ponto 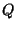 . O potencial criado
pelas cargas
. O potencial criado
pelas cargas 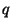 e
e 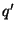 no ponto
no ponto 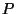 (que é um ponto genérico da
superfície do condutor) é:
(que é um ponto genérico da
superfície do condutor) é:
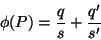 |
(27) |
ou
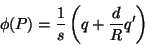 |
(28) |
Se tomarmos
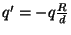 teremos
teremos 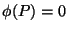 em todos
os pontos da superfície ezférica. Era o que queríamos. Portanto,
o potencial criado por uma carga puntiforme
em todos
os pontos da superfície ezférica. Era o que queríamos. Portanto,
o potencial criado por uma carga puntiforme 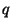 diante de um condutor
esférico aterrado, e distante
diante de um condutor
esférico aterrado, e distante 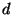 do centro da esfera é, para pontos
externos à esfera, equivalente ao potencial das cargas
do centro da esfera é, para pontos
externos à esfera, equivalente ao potencial das cargas 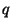 e
e 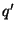 apenas descritas. Ora, o potencial dessas cargas é muito facil de
calcular. De fato, seja
apenas descritas. Ora, o potencial dessas cargas é muito facil de
calcular. De fato, seja 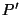 um ponto qualquer fora do condutor, distante
um ponto qualquer fora do condutor, distante
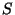 da carga
da carga 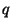 , e
, e 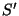 da carga
da carga 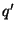 . Temos,
. Temos,
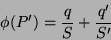 |
(29) |
A partir deste potencial podemos calcular o campo elétrico 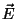 desta mesma distribuição física de cargas e, finalmente, chegar a uma
expressão para a densidade de cargas que se instala na superfície
do condutor por influência da carga externa
desta mesma distribuição física de cargas e, finalmente, chegar a uma
expressão para a densidade de cargas que se instala na superfície
do condutor por influência da carga externa 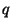 . Estes últimos caálculos
ficam como um exerício facil para o leitor.
. Estes últimos caálculos
ficam como um exerício facil para o leitor.



Next: Apêndice
Up: A magia da equação
Previous: Máximos e mínimos
Henrique Fleming
2002-04-13