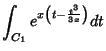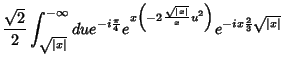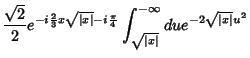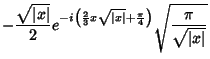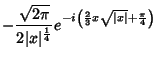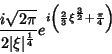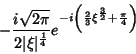Next: Apêndice:O Método do Ponto
Up: O Campo Uniforme
Previous: O Campo Uniforme
As funções descritas pelas Eqs.(35) e (36)
estão expressas como uma representação integral, e, sendo assim,
não se pode ter uma idéia imediata de seu comportamento. Nos casos
em que
 e
e
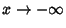 obtêm-se
comportamentos assintóticos mais reveladores. Vamos a eles.
Para
obtêm-se
comportamentos assintóticos mais reveladores. Vamos a eles.
Para 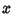 positivo e muito grande na função de Airy (correspondendo
a
positivo e muito grande na função de Airy (correspondendo
a 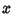 negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
É conveniente voltar à expressão exponencial
negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
É conveniente voltar à expressão exponencial
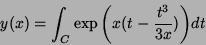 |
(37) |
Pondo
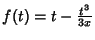 temos
temos
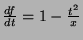 e a condição
e a condição
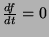 implica em
implica em 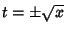 , que são
os possíveis pontos sela. Na região permitida, temos só o valor
, que são
os possíveis pontos sela. Na região permitida, temos só o valor
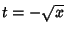 . A seguir faremos a escolha de um caminho de integração
que passe pelo ponto sela e seja de máximo aclive. Na realidade,
é suficiente que o caminho seja de máximo aclive nas
vizinhanças do ponto sela. Vamos então expandir
. A seguir faremos a escolha de um caminho de integração
que passe pelo ponto sela e seja de máximo aclive. Na realidade,
é suficiente que o caminho seja de máximo aclive nas
vizinhanças do ponto sela. Vamos então expandir 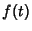 em
série de Taylor em torno de
em
série de Taylor em torno de 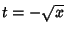 . Temos,
. Temos,
as derivadas sendo calculadas no ponto 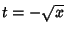 . Facilmente se
obtém que
. Facilmente se
obtém que
e que
Naturalmente a derivada primeira é zero nesse ponto, pois ele é
ponto sela. Então,
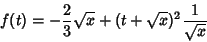 |
(38) |
Para separar as partes real e imaginária de 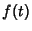 escrevo
escrevo
o que dá
Então, nas vizinhanças de 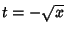 , temos:
, temos:
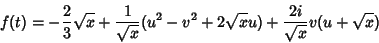 |
(39) |
Considere a reta 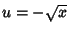 . Ao longo dela,
. Ao longo dela, 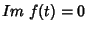 . Logo,
é uma curva de máximo aclive.
. Logo,
é uma curva de máximo aclive.
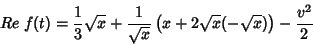 |
(40) |
ou, simplificando,
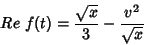 |
(41) |
Então a linha de maior aclive é a paralela ao eixo imaginário
passando por 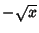 . Pondo
. Pondo
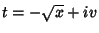 , temos
, temos
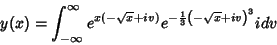 |
(42) |
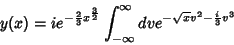 |
(43) |
e podemos omitir a exponencial imaginária do integrando, pois
a parte gaussiana, para grandes valores de 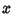 , restringe de tal
forma o trecho do contorno que conta para a integral, que
, restringe de tal
forma o trecho do contorno que conta para a integral, que
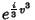 pode ser substituída por seu valor em
pode ser substituída por seu valor em 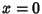 .
Então,
.
Então,
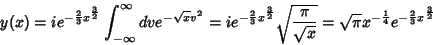 |
(44) |
Levando em conta a definição da função de Airy, temos o comportamento
assintótico
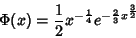 |
(45) |
Como a função de onda do sistema sob a ação do campo uniforme é
o comportamento assintótico que obtivemos é o esperado, uma vez que,
para 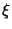 negativo e de grande módulo, estamos na região classicamente
inacessível, e a exponencial negativa é bem-vinda.
Consideremos agora o comportamento assintótico para grandes valores
de
negativo e de grande módulo, estamos na região classicamente
inacessível, e a exponencial negativa é bem-vinda.
Consideremos agora o comportamento assintótico para grandes valores
de 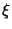 , o que corresponde, na função de Airy, a
, o que corresponde, na função de Airy, a 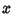 negativo e de
frande módulo. Neste caso
negativo e de
frande módulo. Neste caso
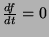 dá
dá
ou seja, 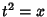 , com
, com 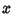 negativo. Então,
negativo. Então,
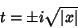 |
(46) |
Aqui os dois pontos sela devem ser considerados, já que estão,
ambos, em regiões onde a integral converge. Vamos, primeiro,
ao ponto 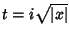 . Expandindo a função
. Expandindo a função
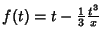 em torno do ponto sela, temos:
em torno do ponto sela, temos:
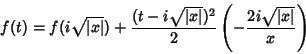 |
(47) |
onde omitimos o termo contendo a derivada primeira, já que ela se anula
no ponto sela. Após um cálculo simples, obtém-se:
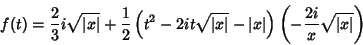 |
(48) |
Usando 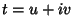 ,
,
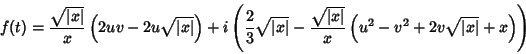 |
(49) |
Segue que
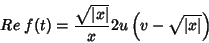 |
(50) |
e
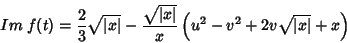 |
(51) |
ou
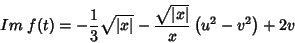 |
(52) |
Ao longo da reta
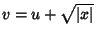 temos
temos
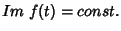 , logo, este
é o primeiro trecho do caminho, aquele que passa pelo ponto sela
, logo, este
é o primeiro trecho do caminho, aquele que passa pelo ponto sela
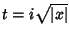 .
Considerações inteiramente análogas levam à conclusão que o
segundo trecho do contorno é a reta
.
Considerações inteiramente análogas levam à conclusão que o
segundo trecho do contorno é a reta
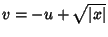 , ou, mais
precisamente, o segmento que começa no eixo real, em
, ou, mais
precisamente, o segmento que começa no eixo real, em 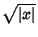 e
vai a
e
vai a 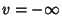 . Assim, o contorno de integração adequado para o
comportamento assintótico para
. Assim, o contorno de integração adequado para o
comportamento assintótico para 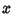 negativo e de grande módulo
é o que está representado na figura abaixo.
negativo e de grande módulo
é o que está representado na figura abaixo.
Contorno para o cálculo do comportamento
assintótico para 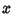 negativo, de grande
negativo, de grande
módulo.
A contribuição do trecho superior do contorno à integral é:
Alguma álgebra elementar leva este resultado à forma:
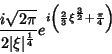 |
(57) |
onde pusemos 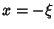 .
A contribuição do outro trecho é perfeitamente análoga, dando como resultado
.
A contribuição do outro trecho é perfeitamente análoga, dando como resultado
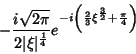 |
(58) |
Somando as duas, temos
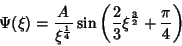 |
(59) |
Vamos nos deter agora um pouco na interpretação física do
resultado, comparando a solução com a solução clássica para o mesmo
problema. É preciso ressaltar que o que calculamos foram as funções
de onda dos estados estacionários de um corpo sob a ação
de uma força constante (queda livre, por exemplo). Classicamente
nunca, ou raramente, estudamos estados estacionários, o que
torna a comparação entre os resultados mais dificil. Para realizar
estados estacionários em queda livre na mecânica clássica, temos
que recorrer a um conjunto de muitas partículas. Um bom modelo de
queda livre em estado estacionário na mecânica clássica é
uma cachoeira sem turbulência, um lençol homogêneo de água
em queda livre. Cada gota de água estará em movimento, mas
o conjunto de todas as gotas forma uma figura que, no conjunto,
parece imóvel. Vamos mostrar que a solução quântica que obtivemos
possui algo em comum com a solução clássica. Isto é mais fácil
de ver usando-se a expressão assintótica
da Eq.(59).
De fato, usando a Eq.(59) temos que
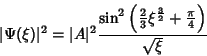 |
(60) |
O sistema clássico correspondente é uma partcxicula de massa 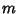 em queda livre (ou, antes, uma enorme quantidade delas). A conservacxa
da energia dá
em queda livre (ou, antes, uma enorme quantidade delas). A conservacxa
da energia dá
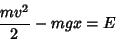 |
(61) |
de onde se tira
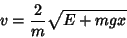 |
(62) |
e, portanto,
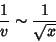 |
(63) |
Para o sistema clássico, a probabilidade de se encontrar a
partcxicula
em torno de uma posicxa 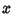 é inversamente proporcional à velocidade dela
naquela posicxa, pois é diretamente proporcional ao tempo que a
partcxicula em torno da posicxa. Quanticamente esta probabilidade é
dada
por
é inversamente proporcional à velocidade dela
naquela posicxa, pois é diretamente proporcional ao tempo que a
partcxicula em torno da posicxa. Quanticamente esta probabilidade é
dada
por 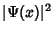 . Comparando a Eq.(60) com a
Eq.(63), vemos que a dependência em
. Comparando a Eq.(60) com a
Eq.(63), vemos que a dependência em 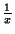 comparece nas duas.
comparece nas duas.



Next: Apêndice:O Método do Ponto
Up: O Campo Uniforme
Previous: O Campo Uniforme
Henrique Fleming
2001-11-22
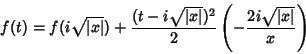
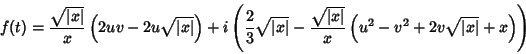
{$-i\sqrt{\vert x\vert}$}
\end{pspicture}](img171.png)