


Next: Vetores e tensores no
Up: Transformações de Lorentz
Previous: Transformações de Lorentz
Chama-se4. Trata-se da
transformação de Lorentz de um sistema de referência 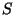 para um outro,
para um outro, 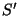 , que tem
os eixos espaciais para lelos aos de
, que tem
os eixos espaciais para lelos aos de 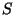 , tem uma velocidade relativa (em relação a
, tem uma velocidade relativa (em relação a 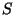 ) de
módulo
) de
módulo 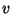 , ao longo da direção positiva dos eixos
, ao longo da direção positiva dos eixos 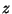 , e tal que a seguinte condição
se verifica: no instante
, e tal que a seguinte condição
se verifica: no instante 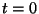 as origens dos dois sistemas de eixos coincidem, e
neste evento (a coincidência espacial das origens,
as origens dos dois sistemas de eixos coincidem, e
neste evento (a coincidência espacial das origens, 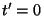 também. Esta é a
transformação de Lorentz mais simples que não é trivial nem se reduz a uma mera
rotação . Como é bem conhecido, ela é dada por:
também. Esta é a
transformação de Lorentz mais simples que não é trivial nem se reduz a uma mera
rotação . Como é bem conhecido, ela é dada por:
onde
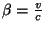 , e
, e
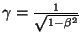 .
Formalmente, temos
.
Formalmente, temos
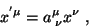 |
(108) |
portanto
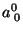 |
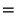 |
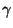 |
(109) |
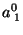 |
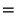 |
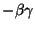 |
(110) |
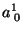 |
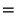 |
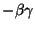 |
(111) |
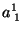 |
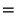 |
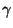 |
(112) |
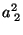 |
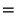 |
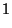 |
(113) |
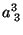 |
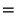 |
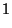 |
(114) |
todos os outros coeficientes sendo nulos.



Next: Vetores e tensores no
Up: Transformações de Lorentz
Previous: Transformações de Lorentz
Henrique Fleming
2002-04-15