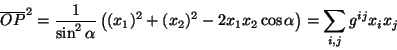Next: Transformações de coordenadas
Up: Introdução aos tensores
Previous: O momento de inércia
Quando se utilizam bases não ortogonais, uma surpresa aparece:
um vetor tem dois tipos diferentes de componentes, chamadas
componentes covariantes e componentes contravariantes.
Isto vem do fato, como mostra a figura, de que podemos identificar
um vetor através de suas projeções nos eixos, de duas maneiras
diferentes: por projeções ortogonais e projeções paralelas
(em eixos ortogonais essas duas projeções coincidem).
O vetor 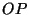 , referido a eixos oblíquos, pode ser caracterizado tanto pelo
par de números
, referido a eixos oblíquos, pode ser caracterizado tanto pelo
par de números 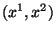 , obtidos por projeção de
, obtidos por projeção de 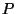 paralelamente
aos eixos, quanto pelo par de números
paralelamente
aos eixos, quanto pelo par de números 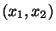 , obtidos por projeção
ortogonal.
, obtidos por projeção
ortogonal.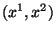 são as coordenadas contravariantes do vetor
são as coordenadas contravariantes do vetor  .
.
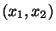 são as coordenadas covariantes. A relação entre elas
é obtida facilmente:
são as coordenadas covariantes. A relação entre elas
é obtida facilmente:
assim como a relação inversa:
O comprimento 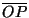 do vetor, em termos de suas componentes
contravariantes, é dado por
do vetor, em termos de suas componentes
contravariantes, é dado por
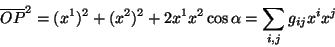 |
(45) |
onde 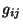 tem os seguintes valores, tabulados como uma matriz:
tem os seguintes valores, tabulados como uma matriz:

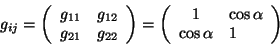 |
(46) |
Usando (77), temos a expressão para 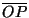 em termos das
componentes covariantes:
em termos das
componentes covariantes:
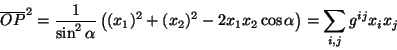 |
(47) |
com
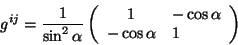 |
(48) |
Vamos, a partir de agora,voltar a usar a notação abreviada: em expressões
do tipo
omitiremos o símbolo da soma (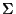 ). Toda vez que tivermos um
índice repetido, como em
). Toda vez que tivermos um
índice repetido, como em 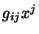 (o
(o 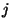 é repetido) somaremos
sobre esse índice, como se houvesse o
é repetido) somaremos
sobre esse índice, como se houvesse o 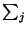 na frente.
Então a Eq.(42) pode ser escrita
na frente.
Então a Eq.(42) pode ser escrita
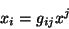 |
(49) |
e a Eq.(77),
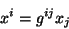 |
(50) |
É claro então que
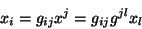 |
(51) |
e, conseqüentemente,
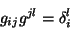 |
(52) |
Isto é, a matriz de elementos 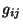 é a inversa da matriz de elementos
é a inversa da matriz de elementos
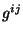 .
Se introduzirmos vetores unitários
.
Se introduzirmos vetores unitários 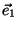 ao longo do eixo
ao longo do eixo 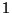 e
e
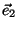 ao longo do eixo
ao longo do eixo 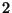 , teremos
, teremos
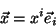 |
(53) |
que define as componentes contravariantes. As componentes covariantes são
definidas por
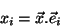 |
(54) |
Usando (53) em (54), temos
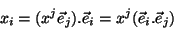 |
(55) |
logo, comparando com (49),
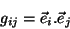 |
(56) |
Subsections



Next: Transformações de coordenadas
Up: Introdução aos tensores
Previous: O momento de inércia
Henrique Fleming
2002-04-15
(3,5)
\psline[line...
...){$x^2$}
\uput[0](2.3,4.8){$x_2$}
\uput[0](0.3,0.8){$\alpha$}
\end{pspicture}](img98.png)
(3,5)
\psline[line...
...){$x^2$}
\uput[0](2.3,4.8){$x_2$}
\uput[0](0.3,0.8){$\alpha$}
\end{pspicture}](img98.png)