


Next: Teorema do divergente
A magia da equação de Laplace
Henrique Fleming
21-8-01
Na eletrostática temos as equações básicas
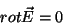 |
(1) |
(que significa que a força eletrostática é conservativa)
e, nas regiões onde não há cargas,
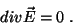 |
(2) |
A primeira dessas equações é equivalente a
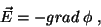 |
(3) |
onde 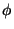 é o potencial escalar. Usando 3 em
2, temos
é o potencial escalar. Usando 3 em
2, temos
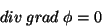 |
(4) |
ou
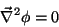 |
(5) |
onde
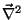 é o operador Laplaceano. A equação
5 é a famosa equação de Laplace. Boa parte
de sua fama é devida a um poderoso teorema de existência
e unicidade que é o tema principal dessas notas. Para demonstrar
esse teorema precisamos do teorema do divergente.
Numa região onde há cargas, não vale a equação de Laplace,
que é substituída pela equação de Poisson,
é o operador Laplaceano. A equação
5 é a famosa equação de Laplace. Boa parte
de sua fama é devida a um poderoso teorema de existência
e unicidade que é o tema principal dessas notas. Para demonstrar
esse teorema precisamos do teorema do divergente.
Numa região onde há cargas, não vale a equação de Laplace,
que é substituída pela equação de Poisson,
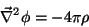 |
(6) |
onde 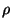 é a densidade volumétrica de carga. Por outro lado,
generalizando a lei de Coulomb, vimos que
é a densidade volumétrica de carga. Por outro lado,
generalizando a lei de Coulomb, vimos que
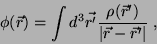 |
(7) |
e que, portanto, a Eq.(7) exibe uma solução da
Eq.(6). De fato, (7) é a solução
de (6) que se anula no infinito. Mais tarde vamos
estudar o método inventado por George Green para obter este
resultado trabalhando diretamente com a equação de Poisson.



Next: Teorema do divergente
Henrique Fleming
2002-04-13